SPOJ.COM - Thuật toán bài NAKANJ - Minimum Knight moves

Posted on September 25th, 2016

Đề bài:

Tít và Mít là đôi bạn tốt. Tuy nhiên, gần đây họ có cãi cọ nhau trong khi chơi cờ vua. Mít muốn biết số bước đi nhỏ nhất để quân mã xuất phát từ 1 ô để đi đến 1 ô khác trên bàn cờ vua 8×8. Tít rất thông minh nên cậu ta đã nghĩ ra thuật toán và viết ra một chương trình để giải quyết bài toán này. Tít đố Mít có thể làm được như vậy.

Tuy nhiên, Mít rất yếu về lập trình nên mong muốn bạn giúp cậu ấy. Quân mã di chuyển theo hình chữ L, chắc bạn cũng biết nên mình không giải thích nhiều nữa. Quân mã phải di chuyển theo cách trên và không được đi ra khỏi bàn cờ. Hình sau minh hoạ bàn cờ, và cách di chuyển của con mã:

spoj-com-thuat-toan-bai-nakanj-minimum-knight-moves

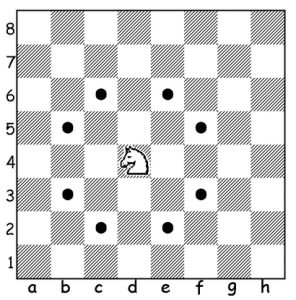
Đầu vào

Có tổng số T test cases. Với mỗi test case, sẽ gồm 2 thành phần. Thành phần thứ nhất là điểm xuất phát của con mã. Và thành phần thứ hai là đích đến của con mã. Mỗi thành phần bao gồm 2 kí tự. Kí tự thứ nhất thuộc 8 kí tự từ 'a' đến 'h'. Kí tự thứ hai thuộc 8 kí tự từ '1' đến '8'.

Đầu ra

In ra số bước tối thiểu mà quân mã cần để đi từ điểm xuất phát đến đích ở các dòng riêng biệt.

Ràng buộc:

1 <= T <= 4096

Ví dụ

Đầu vào:

3 
a1 h8 
a1 c2 
h8 c3

Đầu ra:

6 
1 
4

Bạn có thể tham khảo đề bài tiếng anh và submit code tại: http://www.spoj.com/problems/NAKANJ/

Phân tích

Đây là bài toán tìm đường đi ngắn nhất từ một điểm tới một điểm khác.

Do đó ta sẽ triển khai thuật toán tìm kiếm theo chiều rộng - BFS từ điểm ban đầu. Và lan sang các điểm kề với nó theo 8 hướng mà con mã có thể đi.

Lời giải

Bạn nên tự mình nghĩ ra thuật toán của bài toán trước khi tham khảo code của mình nhé. Hãy phát huy tối đa khả năng sáng tạo của bản thân. Hơn nữa code mình viết ra cũng chưa thật sự tối ưu. Nên rất mong nhận được sự chia sẻ của bạn.

Code C/C++

#include <iostream>
using namespace std;

const int MAX = 100;

int SR, SC, ER, EC;     // Lưu toạ độ hàng, cột của điểm bắt đầu và kết thúc
int Mark[8][8];         // Đánh dấu vị trí con mã

typedef struct Point
{
    int row, col;
    Point(){};
    Point(int r, int c): row(r), col(c){};
}Point;

// Hàng đợi
Point queue[MAX];

// Lần lượt là thông tin và điểm đầu, điểm cuối và độ dài của hàng đợi
int fr, re, leng;

// Mô tả đường đi của con mã
int drow[] = {-2,-1,1,2, 2, 1,-1,-2};
int dcol[] = { 1, 2,2,1,-1,-2,-2,-1};

// Thao tác Enqueue, và Dequeue với hàng đợi vòng
void EnQueue(Point p)
{
    queue[re] = p;
    re = (re + 1) % MAX;
    leng++;
}

Point DeQueue()
{
    Point p = queue[fr];
    fr = (fr + 1) % MAX;
    leng--;
    return p;
}

void BFS()
{
    fr = re = leng = 0;

    EnQueue(Point(SR, SC));
    Mark[SR][SC] = 0;

    while(leng > 0)
    {
        Point p = DeQueue();

        // Nếu gặp đích rồi thì dừng lại
        if(p.row == ER && p.col == EC) break;

        // Kiểm tra 8 hướng đi có thể của con mã
        for(int i = 0; i < 8; i++)
        {
            int r = p.row + drow[i];
            int c = p.col + dcol[i];

            if(r >= 0 && r < 8 && c >= 0 && c < 8 && Mark[r][c] == -1)
            {
                Mark[r][c] = Mark[p.row][p.col] + 1;
                EnQueue(Point(r, c));
            }
        }
    }
}

int main()
{
    ios::sync_with_stdio(false);

    // Comment dòng này trước khi submit
    freopen("input.txt","r",stdin);

    int T;
    cin >> T;

    for(int tc = 0; tc < T; tc++)
    {
        char temp[3];

        // Nhập đầu vào và chuyển sang kiểu int
        cin >> temp;
        SR = temp[0] - 'a';
        SC = temp[1] - '0' - 1;

        cin >> temp;
        ER = temp[0] - 'a';
        EC = temp[1] - '0' - 1;

        for(int i = 0; i < 8; i++)
            for(int j = 0; j < 8; j++)
                Mark[i][j] = -1;

        // Triển khai thuật toán BFS để tìm số bước nhỏ nhất
        // từ vị trí ban đầu đến các vị trí còn lại
        BFS();

        // In kết quả
        cout << Mark[ER][EC] << endl;
    }

    return 0;
}

★ Nếu bạn thấy bài viết này hay thì hãy theo dõi mình trên Facebook để nhận được thông báo khi có bài viết mới nhất nhé:

Spoj
BFS