SPOJ.COM - Thuật toán bài MMATRIX - SHIFT Operator on Matrix

Đề bài:

Cho ma trận A kích thước nxn gồm các số nguyên, ( 0 ≤ i < n, 0 ≤ j < n ). Thao tác SHIFT tại hàng i ( 0 ≤ i < n ) sẽ dịch các số ở hàng i sang phải 1 vị trí và số ở cột cuối cùng sẽ trở về đầu tiên.

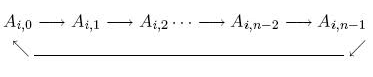
Bạn có thể thực hiện SHIFT bao nhiêu lần cũng được.

Đặt Cj = A0,j + A1,j + ... + A(n-1),j và M = max {Cj|0 <= j < n } sau mỗi lần dịch chuyển. Cj là tổng các số ở cột j.

Tìm giá trị bé nhất của M.

Đầu vào

Gồm một vài test, dòng đầu mỗi test là số nguyên n. n dòng tiếp theo mỗi dòng chứa n số nguyên. Kết thúc các bộ test là số -1. Giả thiết là 1 ≤ n ≤ 7 và |Ai,j| < 10^4.

Ví dụ:

2
4 6
3 7
3
1 2 3
4 5 6
7 8 9
-1

Đầu ra

Với mỗi bộ test, in ra giá trị nhỏ nhất của giá trị lớn nhất của tổng các số trên 1 cột.

Ví dụ:

11
15

Phân tích

Bài này thuộc chủ đề Vét cạn - Brute force nên đương nhiên sẽ phải dùng cách vét cạn. Tuy nhiên, vấn đề là nếu sử dụng thuật toán vét cạn thì độ phức tạp của nó là như thế nào, liệu có bị time limit hay không. Bây giờ, mình sẽ phân tích.

• Bài toán cho SHIFT bao nhiêu lần cũng được, nhưng mình cần phải tính số lần SHIFT sao cho vét cạn được hết tất cả các trường hợp. Vì mỗi hàng của ma trận có n cột, nên ta có các trường hợp dịch với bước nhảy là: 0, 1, 2, ..., n - 1. Chú ý rằng: bước nhảy n sẽ giống với bước nhảy 0, bước nhảy n + 1 sẽ giống với bước nhảy 1,... Như vậy, mỗi hàng sẽ có n trường hợp dịch, mà ta có n hàng. Suy ra: tổng số trường hợp là n ^ n.

• Với mỗi trường hợp dịch như thế, ta phải tìm tổng giá trị của mỗi cột, sau đó suy ra giá trị lớn nhất giữa chúng (M). Và khi đã tìm ra mỗi giá trị lớn nhất này, ta chỉ cần so sánh nó với giá trị nhỏ nhất của M hiện tại để tìm ra giá trị bé nhất của M. Nghĩa là ta phải duyệt toàn bộ ma trận, do đó, độ phức tạp cho công việc này là: n ^ 2.

• Tổng hợp lại: độ phức tạp của thuật toán là: n ^ n x n ^ 2 = n ^ (n + 2).

• Theo bài ra, giá trị lớn nhất của n là 7 => độ phức tạp = 7 ^ (7 + 2) = 7 ^ 9 = 40353607. Mà theo một nghiên cứu, khi độ phức tạp tính ra cỡ 10 ^ 9 thì thời gian thực thi mới hết khoảng 1 giây. Vì vậy, độ phức tạp mà mình tính ra như thế là hoàn toàn khả thi với ràng buộc của bài toán (time limit: 0.131s-1.079s).

Mời bạn theo dõi cách triển khai của mình.

Lời giải

Bạn nên tự mình nghĩ ra thuật toán của bài toán trước khi tham khảo code của mình nhé. Hãy phát huy tối đa khả năng sáng tạo của bản thân. Hơn nữa code mình viết ra cũng chưa thật sự tối ưu. Nên rất mong nhận được sự chia sẻ của bạn.

#include <iostream>
using namespace std;

const int MAX_N = 7;
const int MAX_INT = (2 << 30) - 1;
const int MIN_INT = -(2 << 30);

int N = 0, result;
int A[MAX_N][MAX_N];
int temp[MAX_N];

/**
* Tìm ra giá trị lớn nhất của mỗi cột
*/
int maxOfColumnSum() {
	int M = MIN_INT;

	for (int c = 0; c < N; c++) {
		int colSum = 0;

		for (int r = 0; r < N; r++) {
			colSum += A[r][c];
		}

		if (colSum > M) M = colSum;
	}

	return M;
}

void shift(int r, int step) {
	// copy sang mảng trung gian
	for (int j = 0; j < N; j++) {
		temp[(j + step) % N] = A[r][j];
	}

	// copy ngược lại mảng A giá trị của hàng r sau khi dịch chuyển
	for (int j = 0; j < N; j++) {
		A[r][j] = temp[j];
	}
}

void unshift(int r, int step) {
	// Dịch ngược step đơn vị giống với dịch xuôi (N - step) đơn vị
	shift(r, N - step);
}

void scan(int r) {
	// Điều kiện dừng
	if (r == N - 1) {
		int M = maxOfColumnSum();
		if (M < result) result = M;
		return;
	}

	for (int step = 0; step < N; step++) {
		// Dịch hàng r với bước nhảy step
		shift(r, step);

		scan(r + 1);

		// Trả lại trạng thái của hàng r
		// bằng cách dịch ngược lại với bước nhảy step
		unshift(r, step);
	}
}

int main() {
	//freopen("input.txt", "r", stdin);
	ios::sync_with_stdio(false);

	while (true) {
		// Nhập giá trị của N và ma trận A
		cin >> N;
		if (N == -1) break;

		// Khởi tạo giá trị của result ứng với mỗi test case
		result = MAX_INT;

		for (int i = 0; i < N; i++) {
			for (int j = 0; j < N; j++) {
				cin >> A[i][j];
			}
		}

		// Bắt đầu duyệt đệ quy từ hàng 0 đến hết
		scan(0);

		cout << result << endl;
	}

	return 0;
}