Đây là bài đầu tiên trong chuỗi bài ôn luyện thuật toán trên trang spoj.com mà mình đã làm. Và sau đây là đề bài mà mình đã dịch từ tiếng anh sang tiếng việt. Vì mình chủ yếu là tự học tiếng anh, nên có thể dịch nghĩa chưa được chuẩn xác lắm. Mong bạn thông cảm.
Đề bài:
Cho một lưới hai chiều gồm các kí tự. Yêu cầu tìm ra đường đi dài nhất của các kí tự liên tiếp, bắt đầu tại 'A'. Đường đi có thể nhảy từ 1 kí tự trên lưới đến một kí tự khác theo chiều ngang, dọc hay chéo.
Ví dụ: ở hình sau đây, có một vài đường đi từ A đến D, nhưng không có đường nào đi từ A đến E:

Một trong các đường đi từ A đến D là:
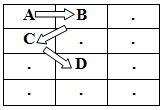
Đầu vào
Mỗi test case sẽ bắt đầu với một dòng gồm 2 số nguyên H, W lần lượt là chiều cao, và chiều rộng của lưới, với 1 <= H, W <= 50. Tiếp theo đó là H dòng, mỗi dòng sẽ có W kí tự viết in hoa. Đầu vào kết thúc với H = W = 0.
Đầu ra
Với mỗi test case in ra "Case C: x" (không có dấu ngoặc kép). Trong đó, C là số thứ tự của test case bắt đầu từ 1 và x là độ dài đường đi dài nhất tìm được.
Ví dụ
Đầu vào:
4 3
ABE
CFG
BDH
ABC
0 0
Đầu ra:
Case 1: 4
Bạn có thể tham khảo link gốc đề bài và submit code tại đây: http://www.spoj.com/problems/ABCPATH/
Phân tích
Thực ra đây là bài toán tìm đường đi. Ta sẽ tìm tất cả các kí tự 'A' trên lưới, sau đó tìm đường đi từ vị trí đó thoả mãn yêu cầu bài toán - Một chú ý ở đây đó là: nếu chúng ta tìm tất cả đường đi có thể thì khả năng cao sẽ dẫn đến time limit.
Bạn có thể thấy bài toán này có đặc điểm là: khi có 2 đường mà trong quá trình đi của nó cùng đi qua một điểm, thì thực chất 2 đường đó sẽ có độ dài như nhau. Ví dụ có 2 đường cùng đi đến điểm C, thì nghĩa là trước đó cả hai đều phải đi qua điểm A và B.
Vì vậy, với bài toán này ta sẽ sử dụng thuật toán tìm kiếm theo chiều sâu - DFS.
Lời giải
Bạn nên tự mình nghĩ ra thuật toán của bài toán trước khi tham khảo code của mình nhé. Hãy phát huy tối đa khả năng sáng tạo của bản thân. Hơn nữa code mình viết ra cũng chưa thật sự tối ưu. Nên rất mong nhận được sự chia sẻ của bạn.
Code C/C++
#include <iostream>
using namespace std;
const int MAX = 51;
int H; // Lưu chiều cao lưới
int W; // Lưu chiều rộng lưới
int Answer; // Kết quả đường đi dài nhất
char Matrix[MAX][MAX]; // Lưu lưới các kí tự
bool Visit[MAX][MAX]; // Đánh dấu trạng thái kí tự được thăm hay chưa
int drow[8] = {-1,-1,0,1,1, 1, 0,-1};
int dcol[8] = { 0, 1,1,1,0,-1,-1,-1};
/*
* row : là chỉ số hàng của điểm hiện tại
* col : là chỉ số cột của điểm hiện tại
* leng: là độ dài đường đi hiện tại
*/
void Start(int row, int col, int leng)
{
// Kiểm tra 8 hướng kề với điểm hiện tại.
for(int i = 0; i < 8; i++)
{
int r = row + drow[i];
int c = col + dcol[i];
/*
* Ô tiếp theo nhảy tới phải thoả mãn điều kiện:
* Nằm trong ma trận
* Chưa được thăm
* Phải là kí tự kế tiếp của kí tự hiện tại theo thứ tự A,B,C,...
*/
if (r >= 0 && r < H && c >= 0 && c < W &&
Visit[r][c] == 0 && Matrix[r][c] == Matrix[row][col] + 1)
{
Visit[r][c] = 1;
Start(r, c, leng+1);
}
}
// Khi không thể đi được nữa, ta sẽ cập nhật kết quả
if(leng > Answer)
{
Answer = leng;
}
}
int main()
{
ios::sync_with_stdio(false);
// comment dòng này trước khi submit
freopen("input.txt","r",stdin);
int tc = 0;
while(true)
{
// Nhập đầu vào
cin >> H >> W;
if(H == 0 && W == 0) break;
tc++;
Answer = 0;
for(int i = 0; i < H; i++)
cin >> Matrix[i];
for(int i = 0; i < H; i++)
for(int j = 0; j < W; j++)
Visit[i][j] = false;
// Tìm kiếm kí tự 'A', và bắt đầu tìm đường đi từ đó
for(int i = 0; i < H; i++)
for(int j = 0; j < W; j++)
if(Matrix[i][j] == 'A')
{
Visit[i][j] = true;
// Bắt đầu tại điểm có toạ độ (i, j)
// và độ dài đường đi lúc này là 1
Start(i, j, 1);
}
// In kết quả
cout << "Case " << tc << ": " << Answer << endl;
}
return 0;
}★ Nếu bạn thấy bài viết này hay thì hãy theo dõi mình trên Facebook để nhận được thông báo khi có bài viết mới nhất nhé:
- Facebook Fanpage: Ôn luyện thuật toán
- Facebook Group: Hỏi đáp thuật toán VN